Similarity of Triangles by SAS Criteria












Similarity of Triangles by SAS Criteria
Similarity of Triangles by SAS Criteria:
Theorem: If in two triangles one pair of corresponding sides are proportional and the included angles are equal then the two triangles are similar.
Given in To Prove Construction: Cut DX equal to AB and DY equal to AC. Join XY Proof: It has been given Replacing Ab with DX and AC with DY Taking Reciprocal and subtracting 1 from both sides
AB = DX [By Construction ] AC = DY [By Construction ]
From Eq (1) and (2) Therefore
|
|
Illustration: If AD and PM are medians of triangles ABC and PQR respectively where | |
Solution: Given
As AD and PM are the medians so
BC= 2BD=2CD and QR= 2 QM= 2MR ......................(2) From Eq 1
Thus Hence Proved | 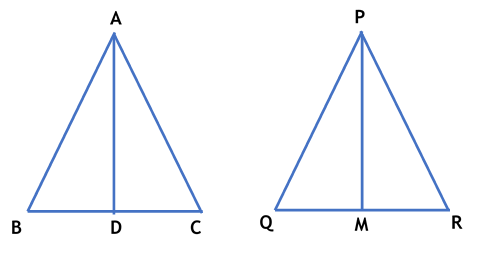 |
In the following figure, ABC is a triangle in which AB = AC, D and E are points on the sides AB and AC respectively, such that AD = AE. Then
| |||
| Right Option : D | |||
| View Explanation | |||
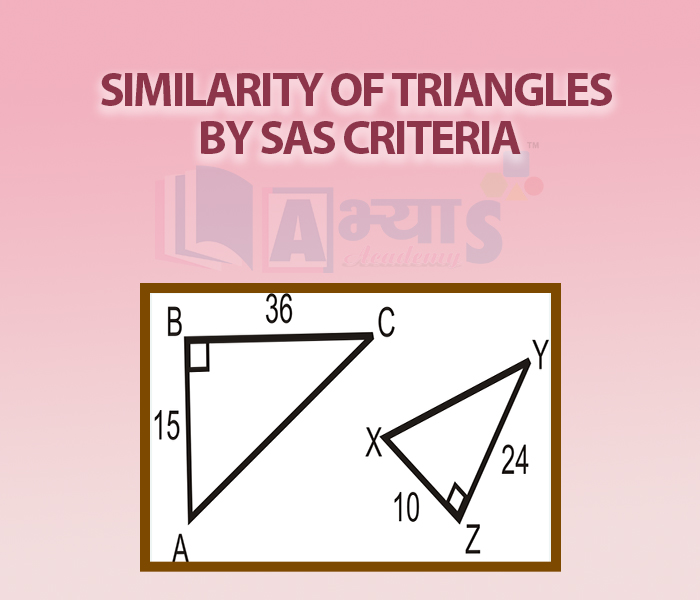
Find the value of x if the triangles are similar by SAS criteria. | |||
| Right Option : C | |||
| View Explanation | |||
In the following figure, AB || QR. Find the length of PB.
| |||
| Right Option : D | |||
| View Explanation | |||
Students / Parents Reviews [10]
It has a great methodology. Students here can get analysis to their test quickly.We can learn easily through PPTs and the testing methods are good. We know that where we have to practice

Barkha Arora
10thMy experience with Abhyas academy is very good. I did not think that my every subject coming here will be so strong. The main thing is that the online tests had made me learn here more things.

Hiya Gupta
8thOne of the best institutes to develope a child interest in studies.Provides SST and English knowledge also unlike other institutes. Teachers are co operative and friendly online tests andPPT develope practical knowledge also.

Aman Kumar Shrivastava
10thBeing a parent, I saw my daughter improvement in her studies by seeing a good result in all day to day compititive exam TMO, NSO, IEO etc and as well as studies. I have got a fruitful result from my daughter.

Prisha Gupta
8thIt was good as the experience because as we had come here we had been improved in a such envirnment created here.Extra is taught which is beneficial for future.

Eshan Arora
8thI have spent a wonderful time in Abhyas academy. It has made my reasoning more apt, English more stronger and Maths an interesting subject for me. It has given me a habbit of self studying

Yatharthi Sharma
10thMy experience was very good with Abhyas academy. I am studying here from 6th class and I am satisfied by its results in my life. I improved a lot here ahead of school syllabus.

Ayan Ghosh
8thAbout Abhyas metholodology the teachers are very nice and hardworking toward students.The Centre Head Mrs Anu Sethi is also a brilliant teacher.Abhyas has taught me how to overcome problems and has always taken my doubts and suppoeted me.

Shreya Shrivastava
8thMy experience with Abhyas is very good. I have learnt many things here like vedic maths and reasoning also. Teachers here first take our doubts and then there are assignments to verify our weak points.

Shivam Rana
7thA marvelous experience with Abhyas. I am glad to share that my ward has achieved more than enough at the Ambala ABHYAS centre. Years have passed on and more and more he has gained. May the centre flourish and develop day by day by the grace of God.